Bei physikalischen und elektronischen Arbeiten ist oft eine Berechnung des Leitungswiderstands nötig. Die wichtigen Hintergründe hierzu und auch einige Formeln werden hier näher erläutert.
In welchen Bereichen spielt der Leiterwiderstand eine Rolle?
Der Leitungswiderstand spielt eine bedeutende Rolle im Zusammenhang mit Projekten der Elektrotechnik. Dieser Widerstand wirkt sich direkt auf den Kabelverlust aus. Die Leistung eines Kabels richtet sich nach Daten wie der Länge, den Querschnitt, der Eingangsspannung sowie der Gesamtlast. Von der Spannung, die an der Quelle in die Leitung hineinkommt, geht auf dem Weg zum Verbraucher ein gewisser Anteil verloren. Genau dabei geht es bei dem Kabelverlust.
Durch die Berechnung des Leitungswiderstands kann man den Kabelverlust ebenfalls kalkulieren und gegebenenfalls spezielle Maßnahmen ergreifen, um eine bessere Leistung zu erzielen. Typische Einsatzbereiche, bei denen es auf eine optimale Leistungsübertragung ankommt, sind:
- Hausanschlüsse,
- Solaranlagen,
- Überlandleitungen,
- Kommunikationsversorgung (Telefonie und Internet),
- Multimedia-Bereich.

Durch die Berechnung des Leitungswiderstands kann man den Kabelverlust ebenfalls kalkulieren und gegebenenfalls spezielle Maßnahmen ergreifen, um eine bessere Leistung zu erzielen. (#01)
Warum der Leitungswiderstand so relevant ist
Der Verlust der Spannung wirkt sich direkt auf das Potenzial eines Stromkreises aus. Häufig wird vernachlässigt, dass auch die Stromkabel zu den elektrischen Verbrauchern zählen und daher die Stromspannung absinken lassen.
Bei der Generierung einer Elektroanlage muss man daher die Kabelverluste genau einplanen, damit die Funktion später nicht beeinträchtigt wird. Aus diesem Grund ist eine genaue Berechnung des Leitungswiderstands nötig, und zwar schon am Anfang der Projektplanung. Wenn diese Kalkulation fehlt, kommt es in der Folge zu Schwierigkeiten, die nur durch einen relativ großen Aufwand wieder korrigiert werden können.
Im Folgenden sollen einige Fälle näher beschrieben werden, bei denen der mögliche Kabelverlust unbedingt berechnet werden sollte.
Kabel der Spannungsversorgung
Wenn es zu einem Leitungsverlust in einem Spannungsversorgungskabel kommt, so sind zwei Auffälligkeiten zu beobachten: Auf der einen Seite erwärmt die anfangs hohe Belastung das Kabel, was bis zu einer thermischen Überlastung führen kann, die wiederum die Isolation oder die nahen Komponenten beschädigen kann. So eine Überlastung erhöht das Risiko, dass es zu einem Stromschlag oder sogar zu einem Brand kommt.
Andererseits kommt beim angeschlossenen Verbraucher zu wenig Stromspannung an, denn der Leitungswiderstand hat diese auf dem Weg dorthin stark verringert. Die meisten Elektrogeräte haben deshalb eine gewisse Toleranz, sodass sie auch bei einer etwas geringeren Spannung richtig funktionieren. Wenn die Spannungsleistung jedoch unter den Mindestwert dieses Toleranzbereichs fällt, dann arbeiten die Geräte nicht mehr optimal.

Eine Überlastung erhöht das Risiko, dass es zu einem Stromschlag oder sogar zu einem Brand kommt. (#02)
Kabelleitungen in Kommunikations- und Multimedial-Anlagen
Bei einem Leitungsverlust in einer Kommunikationsanwendung spricht man auch von einer Dämpfung. Typische Fehler, die durch eine zu geringe Spannungsleistung entstehen, sind ein Rauschen des Tonsignals oder eine Störung im Bild.
Wenn die Übertragungsfrequenz ansteigt, erhöht sich zugleich der Anspruch an die optimale, möglichst verlustarme Stromleitung. Das ist beispielsweise bei dem Internetzugang der Fall. Veraltete Datenleitungen haben oft einen zu hohen Verlust, sodass die Übertragungsrate entsprechend gering ist.
Die modernen Leitungssegmente zeigen sich deutlich verlustärmer. In der heutigen Zeit sollte ein guter Ausbau der Elektro- und Kommunikationskabel im Allgemeinen der Standard sein. Die Berechnung des Leistungswiderstands zeigt auf, wo es eventuell noch Schwachstellen gibt.
Details zum Kabelverlust
Beim Kabel- oder Leitungsverlust kann es sich um zwei unterschiedliche Arten handeln. Diese sollen in diesem Abschnitt kurz beschrieben werden. Grundsätzlich treten beide Verlustarten gemeinsam auf. Es gibt allerdings verschiedene Betriebsbedingungen, die sich auf die Aufteilung auswirken:
- die physische Kabelverlegung,
- benachbarte Werkstoffe und Bauteile,
- Strom- und Spannungsstärke,
- elektrische Signalfrequenz.
Die Ohmschen Verluste sind die bekanntere Verlustart. Hier steht einem das Ohmsche Gesetz zur Verfügung, das folgendermaßen aussieht:
R = U/I
Die daraus entwickelte Formel zur Berechnung dieses Leitungswiderstands ist:
P = U*I
Dabei ist R der elektrische Widerstand, U die elektrische Spannung, I der elektrische Strom und P die elektrische Leistung. Die Verlustleistung hängt hauptsächlich von der Höhe des elektrischen Stroms ab.
Die frequenzabhängigen Verluste sind abhängig von Schwankungen der Betriebsfrequenz oder von der belastungsabhängigen Phasenlage zwischen Energie und Spannung. Mit dieser Erklärung grenzen sich die frequenzabhängigen Verluste von den Ohmschen Verlusten ab. Die Berechnungsformel kann deshalb nur für den Gleichspannungsbereich eingesetzt werden oder gegebenenfalls für Wechselspannung ohne Phasenverschiebung.
Hintergründe zum Leitungsverlust
Ein Leitungswiderstand ist nach dem Ohmschen Gesetz zu behandeln, wenn er keine Abhängigkeit zu Stromspannung, Stärke und Frequenz zeigt. Das zeigt sich bei der Darstellung in einem Diagramm.
Zwischen der Spannungs- und Stromstärkenlinie entsteht eine Ursprungsgerade. Eine Komponente mit Ohmschen Widerstandswert führt dazu, dass sich die abfallende Stromspannung proportional zur Stromstärke und zum Anstiegswert der Geraden verhält. Hier kommt der Proportionalitätsfaktor R zum Einsatz.
Bei dem Kehrwert des Ohmschen Widerstandswerts, der den Proportionalitätsfaktor zwischen Stromstärke und Energiespannung angibt, handelt es sich um den elektrischen Leitwert G.
Der Ohmsche Widerstandswert lässt sich durch ein bestimmtes Bauteil wie einen Draht realisieren, das oft einfach als Widerstand bezeichnet wird.
Beim Stromfluss durch ein Widerstandselement und dem Spannungsabfall kommt es zur Umwandlung von Elektroenergie in Wärme.
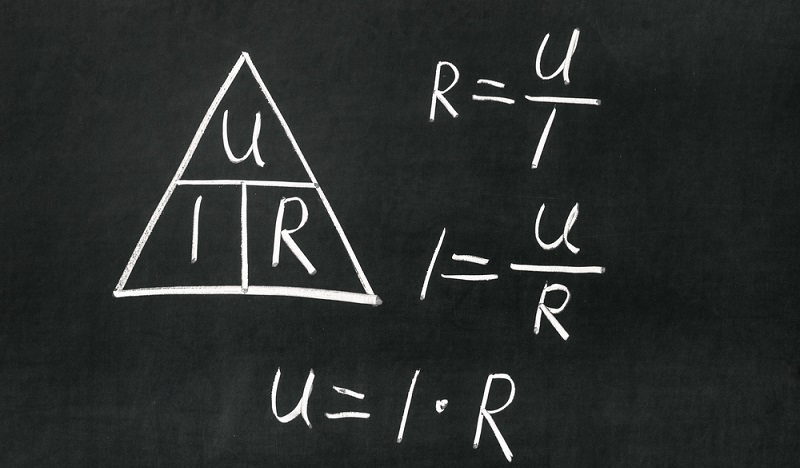
Ein Leitungswiderstand ist nach dem Ohmschen Gesetz zu behandeln, wenn er keine Abhängigkeit zu Stromspannung, Stärke und Frequenz zeigt. (#03)
Berechnung des Leitungswiderstands: So geht man dabei vor
Für die Berechnung des Leitungswiderstands müssen viele Daten berücksichtigt werden. Neben Querschnitt, Länge und anderen Rahmenbedingungen braucht man eine geeignete Formel. Die Beschaffenheit der Leitung spielt eine wesentliche Rolle für den Leiterwiderstand. Ebenfalls wichtig ist der spezifische Widerstand, bei dem es sich um eine temperaturabhängige Konstante handelt. Er wird durch das Zeichen ρ (Rho) angegeben und definiert den Leitungswiderstand des 1 m langen Stoffes bei einer Querschnittsfläche von 1mm². Bei konstanter Leitertemperatur gilt die Formel:
R = ρ*l/A
R steht hier für den Leiterwiderstand in Ohm,
ρ ist der spezifische Widerstand in Ohm * mm²/m,
l ist die Leiterlänge in m.
A ist die Querschnittsfläche in mm²
Für die Berechnung des Querschnitts A von runden Stromleitern verwendet man die Formel:
A = 0,25 π d2.
Video: Ohmsches Gesetz und Widerstände
Eine Beispielsrechnung
In dem folgenden Beispiel lässt sich die Berechnung gut nachvollziehen:
Für einen 300 m langer Kupferleiter mit einem Querschnitt von 300 mm² soll der Leitungswiderstand bei einer Durchschnittstemperatur von 20 Grad errechnet werden. Den spezifischen Widerstand der Kupferleitung findet man in einem Tabellenblatt. Mit diesen Daten in der Formel ist eine gezielte Berechnung vom Leitungswiderstand möglich:
l = 200 m
A = 200 mm²
ρ = 0,017 Ω * mm²/m
R = ρ*l/A
R = 0,017 Ω * mm²/m * 200 m/200 mm² = 0,017 Ω
Leitungswiderstand: Nicht nur in der Elektrotechnik wichtig
Die Berechnung vom Leitungswiderstand sollte nicht nur bei Großanlagen durchgeführt werden. Auch kleine Geräte können in ihrer Funktion eingeschränkt werden, wenn man den möglichen Kabelverlust unterschätzt. Daher lohnt es sich, genau auf die Qualität der Kabel zu achten und gegebenenfalls die Leitungen zu kürzen, um den Verlust zu reduzieren. Der Leitungswiderstand könnte sich sonst nachteilig auf die Leistung des Elektrogeräts auswirken.
In der Physik und in der Elektrotechnik geht es um die genaue Kalkulation der Leistungs- und Verlustdaten. Im alltäglichen Einsatz wünscht man sich einfach funktionierende Apparate. Wer die wichtigen Daten im Kopf behält, der weiß, worauf er bei der Installation von Elektronik achten muss. Und wer beruflich mit damit zu tun hat, der kennt sich ohnehin mit den entsprechenden Formeln und den nötigen Maßnahmen zur Verbesserung der Leistung aus.
Bildnachweis:© Shutterstock – Titelbild: drawhunter – #01: GeoArt – #02: herjua – #03: Jurgis Mankauskas














